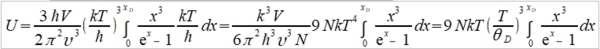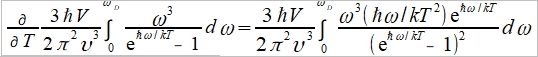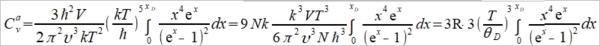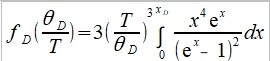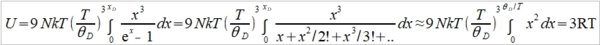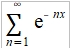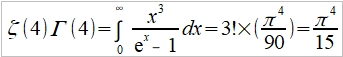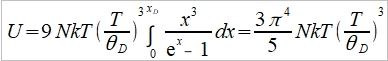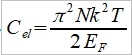字體:小 中 大
字體:小 中 大 |
|
|
|
| 2023/02/07 12:15:04瀏覽695|回應2|推薦0 | |
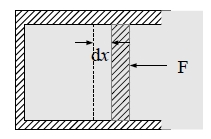
合金熱力學基礎 熱力學是研究過程是否自發進行?在甚麼條件下能達到平衡?掌握和利用這些客觀規律,幫助我們控制轉變,控制結構與成分,從而改變金屬和合金的性能。 第一定律:系統的內能增量dU 等於由環境進入系統的熱能δQ和系統對環境所做的功δW的差 dU=δQ-δW...(1) 內能的改變量完全由始態和終態決定,與A到B的過程無關,所以內能是狀態函數;而Q與W是與過程的途徑有關,不是狀態性質。 如果系統對環境做功, δW=Fdx=PAdx=PdV, 因而dU=δQ-PdV...(2)
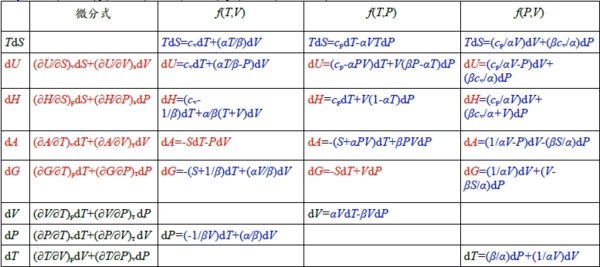
兩邊除以dT, 得 dU/dT=δQ/dT-PdV/dT 如果系統的體積固定, 則dV/dT=0, 所以定容比熱Cᵥ: Cᵥ=(δQ/dT)ᵥ=(∂U/∂T)ᵥ 實驗過程通常都在定壓下做試驗,所以引入另一狀態函數,焓(H) H≡U+PV → 進行微分 dH=dU+PdV+VdP 將(2)代入 dH=δQ+VdP 兩邊除以dT, 得 dH/dT=δQ/dT+VdP/dT 如果壓力固定, 則Cₚ=(δQ/dT)ₚ=(∂H/∂T)ₚ Cₚ>Cᵥ 因為Cₚ除升高所需溫度外, 還需用在定壓膨脹的功;而Cᵥ只要升高系統的溫度。 熵和第二定律: 幫助我們判斷一個過程是否可以進行,而焓變則不能判斷。 ex. 白錫→灰錫 at 298K ∆H=-0.5 Kcal/g 白錫還是穩定的 可逆過程是一無限緩慢的過程,中間是一系列平衡狀態;在反向的同樣緩慢過程中,按照原來的路徑,使系統和環境完全恢復原來狀態。 熵S: dS=dQ/T (可逆) ex. at 13℃(286K) 恆溫恆壓下, gray Sn ↔ white Sn 可逆過程 由dH=δQ+VdP, 恆壓下, dH=δQ ⸫ dS=dH/T → ∫灰錫白錫dS=∫灰錫白錫dH/T ∆S(系統)=∆H(系統)/T=500/286=1.75 cal/g; ∆H(系統)=-∆H(環境) ⸫ ∆S(環境)=∆H(環境)/T=-1.75 → ∆S(系統)+∆S(環境)=0 對於不可逆過程, Ag₍ₗ₎ → Ag₍ₛ₎ at 800℃, 熔解熱∆Hᶠ₍₁₂₃₄₎=2.69 Kcal/g 因為過冷液態銀凝結後,反向熔解不可能發生,除非溫度升高≥961℃;所以必須分解過程來計算系統的熵變 (1)Ag₍ₗ, ₁₀₇₃ᴷ₎ → Ag₍ₗ, ₁₂₃₄ᴷ₎ ∆S₁ (2)Ag₍ₗ, ₁₂₃₄ᴷ₎ → Ag₍ₛ, ₁₂₃₄ᴷ₎ ∆S₂ (3)Ag₍ₛ, ₁₂₃₄ᴷ₎ → Ag₍ₛ, ₁₀₇₃ᴷ₎ ∆S₃ (1)+(2)+(3) Ag₍ₗ, ₁₀₇₃ᴷ₎ → Ag₍ₛ, ₁₀₇₃ᴷ₎ ∆S(系統)=∆S₁+∆S₂+∆S₃因為熵也是狀態函數 ∆S₁=∫10731234Cₚ,ₗdT/T, ∆S₂=-∆Hᶠ₍₁₂₃₄₎/T, ∆S₃=∫12341073Cₚ,ₛdT/T ⸫∆S(系統)=∫10731234(Cₚ,ₗ-Cₚ,ₛ)dT/T-∆Hᶠ₍₁₂₃₄₎/T, Cₚ₍ₗ₎-Cₚ₍ₛ₎=∆a+∆bT+∆cT⁻² 代入得 ∆S(系統)=-2.2 cal/gK 對於環境可視為一大的貯熱器, 熔解熱∆Hᶠ的變化不會改變它的溫度800℃, 所以 ∆S(環境)=∆Hᶠ₍₁₀₇₃ᴷ₎/1073, ∆Hᶠ₍₁₀₇₃ᴷ₎=∆H₁+∆H₂+∆H₃=-∫10731234(Cₚ,ₗ-Cₚ,ₛ)dT+∆Hᶠ₍₁₂₃₄₎=2715 cal/g ∆S(環境)=2.53 cal/gK, ∆S(系統)+∆S(環境)=0.33 cal/gK >0 由以上二例,得出(a)對可逆過程: ∆S(系統)+∆S(環境)=0 (b)對自發過程: ∆S(系統)+∆S(環境)>0 (c)對不能進行的過程: ∆S(系統)+∆S(環境)<0 span=""> 熱力學第二定律可表述為,在自發過程中,一個孤立體系的熵增加。 自由能函數: ∆S(系統)+∆S(環境)可以判斷過程是否可以進行,但熵變計算不方便,引入自由能 由第二定律 自發過程∆S(系統)+∆S(環境)>0...(3), 雖然過程不可逆,但熱量傳輸是可逆的 ∆S(環境) =δQ/dT(系統→環境)=-δQ/dT(環境→系統), 恆壓下, dH=δQ代入 ∆S(環境) =-dH/dT(環境→系統)代入(3) ∆S(系統)-dH/dT(環境→系統)>0 ⸫ dH-TdS(系統)<0... span="" style="font-family:times new roman , times" data-mce-style="font-family: times new roman , times;">(4) 自發過程 因此定義 dG= dH-TdS, 若在恆溫下, G=H-TS 稱作Gibbs free energy 若過程在定容下進行, dU=δQ, dA= dU-TdS, 若在恆溫下, A=U-TS 稱作Helmholtz free energy 對可逆過程, 能量函數定義: A≡U-TS, H≡U+PV, G≡H-TS 微分式 dU=TdS- PdV...(5) dH=TdS+VdP...(6) dA=-SdT-PdV...(7) dG=-SdT+VdP...(8) 熱力學的數學推導(係數關係) dU=TdS- PdV=(∂U∕∂S)ᵥdS+(∂U∕∂V)ₛdV, T=(∂U∕∂S)ᵥ=(∂H∕∂S)ₚ dH=TdS+VdP=(∂H∕∂S)ₚdS+(∂H∕∂P)ₛdP, S=-(∂A∕∂T)ᵥ=-(∂G∕∂T)ₚ dA=-SdT-PdV=(∂A∕∂T)ᵥdT+(∂A∕∂V)ᴛdV, P=-(∂U∕∂V)ₛ=-(∂A∕∂V)ᴛ dG=-SdT+VdP=(∂G∕∂T)ₚdT+(∂G∕∂P)ᴛdP, V=(∂H∕∂P)ₛ=(∂G∕∂P)ᴛ Maxwell relation : if Z=Z(x,y), dZ=(∂Z∕∂x)ydx+(∂Z∕∂y)xdy=Ldx+Mdy and (∂L∕∂y)x=(∂M∕∂x)y ∴(∂T∕∂V)ₛ=-(∂P∕∂S)ᵥ, (∂T∕∂P)ₛ=(∂V∕∂S)ₚ, (∂S∕∂V)ᴛ=(∂P∕∂T)ᵥ, -(∂S∕∂P)ᴛ=(∂G∕∂T)ₚ
ratio relation z=z(x, y), (∂x∕∂y)z(∂y∕∂z)x(∂z∕∂x)y=-1 pf: dz=(∂z∕∂x)ydx+(∂z∕∂y)xdy → dz/[(∂z∕∂x)y]=dx+(∂z∕∂y)xdy/[(∂z∕∂x)y]=dx+(∂z∕∂y)x(∂x∕∂z)ydy ...(a) x=x(y, z), dx=(∂x∕∂y)zdy+(∂x∕∂z)ydz ...(b), 比較(a),(b) → (∂x∕∂y)z=-(∂z∕∂y)x(∂x∕∂z)y 利用倒數關係, (∂x∕∂y)z(∂y∕∂z)x(∂z∕∂x)y=-1 expansion coeff. α=(1/V)(∂V∕∂T)ₚ, compressibility β=(-1/V)(∂V∕∂P)ᴛ Cₚ-Cᵥ=(∂U∕∂V)ᴛ(∂V∕∂T)ₚ+P(∂V∕∂T)ₚ=(∂V∕∂T)ₚ[P+(∂U∕∂V)ᴛ] ⸪dA=-SdT-PdV ⸫(∂A/∂V)ᴛ=-P, and A≡U-TS (∂A/∂V)ᴛ=(∂U/∂V)ᴛ-T(∂S/∂V)ᴛ=(∂U/∂V)ᴛ-T(∂P/∂T)ᵥ → -P=(∂U/∂V)ᴛ-T(∂P/∂T)ᵥ代入eq. 2-8, Cₚ-Cᵥ=T(∂V∕∂T)ₚ(∂P/∂T)ᵥ ⸪(∂P∕∂T)ᵥ(∂T∕∂V)ₚ(∂V∕∂P)ᴛ=-1 → (∂P∕∂T)ᵥ=-(∂V∕∂T)ₚ/(∂V∕∂P)ᴛ=-αV/-βV=α/β ⸫Cₚ-Cᵥ=T(∂V∕∂T)ₚ(∂P/∂T)ᵥ=-T(∂V∕∂T)²ₚ/(∂V∕∂P)ᴛ=α²VT/β
**當然也可轉換成f(S,V)或f(P,S),不過溫度、壓力、體積是實驗可操作的變數 Dulong-Petit規律: 高於室溫下, Cᵥ=3R≈6 cal/gK and α²VT/β=0.5 cal/gK, 因而Cₚ=6.5 cal/gK. 反應過程產生的功: 一是機械功PdV; 另一是有用功δW, 如電能. 所以總功δW可寫為 δW=PdV+δW 代入第一定律 dU=δQ-δW=δQ-PdV-δW 如果是可逆過程, δQ=TdS, dU=TdS-PdV-δW, 又因 dA=dU-TdS-SdT, ⸫dA=-SdT-PdV-δW 在恆溫下進行, 即dT=0, -dA=PdV+δW → -∆A=∫₁²(PdV+δW)=Wₘₐₓ 因此在恆溫的可逆過程中系統對外做的最大總功等於自由能減少的部分;若是不可逆,做功小於Wₘₐₓ, (1)恆溫且δW=0, -∆A=∫₁²PdV, (2)恆溫且體積不變, δW≠0, -∆A=∫₁²δW=W 同理, -∆G=-∫₁²VdP+∫₁²δW, (1)恆溫且δW=0, -∆G=-∫₁²VdP, (2)恆溫且壓力不變, δW≠0, -∆G=∫₁²δW=W 自由能A或G可以釋放出來做功,在相轉變中,他們是推動轉變的驅動能 熵的統計理論: S=klnW 在一個自發反應中, 孤立系統的熵會增加, 當達到平衡時, 其熵達到最高值; 統計熱力學以為系統處於亂度最大的可能機率的選擇數目W,與系統的熵有一定的關係: S=klnW ex. 8個小球均勻分布于4個匣子,即2-2-2-2這樣一種分布的熱力學機率的選擇數目 W= 推廣至一般情形, N個粒子進入V₁, V₂,..., Vᵢ個匣子,粒子分布為N₁, N₂,..., Nᵢ的宏觀態,其熱力學機率的選擇數目, W=N!/(N₁!N₂!...Nᵢ!) 取對數, lnW=lnN!-(lnN₁!+lnN₂!+...+lnNᵢ!) i.e. 當N>>1, lnN!≈NlnN-N → lnW=NlnN-N-∑(NᵣlnNᵣ-Nᵣ) ⸪ 混合熵∆Sₘ: 考慮A, B兩元混合的固溶體,假定原子在晶體中的分布是完全雜亂;晶體有N個原子, A和B的原子數分別為N-n, 及n. (i.e. Xᴀ=(N-n)/N, Xᴃ=n/N Xᴀ+Xᴃ=1) 形成固溶體的系統熵增量為 ∆Sₘ=Sᴀᴃ-Sᴀ-Sᴃ=k(lnWᴀᴃ-lnWᴀ-lnWᴃ) 因為Wᴀᴃ=N!/[n!(N-n)!], Wᴀ=(N-n)!/(N-n)!=1, Wᴃ=n!/n!=1 所以∆Sₘ=kln{N!/[n!(N-n)!]} ∆Sₘ= k[lnN!-lnn!-ln(N-n)!]≈k[NlnN-nlnn-(N-n)ln(N-n)]=-Nk(XᴀlnXᴀ+XᴃlnXᴃ) 晶體比熱和振動熵 晶體在加熱過程中吸收的熱量,一方面使能量接近費米能的少數電子的動能增加,表現為電子比熱,Cᵥᵉ; 另一方面使原子的晶格振動能量增加,表現為振動比熱Cᵥᵃ. 比熱在常溫以上是一個與溫度無關的常數(Cᵥ≈3R=5.96 cal/gK), 但在低溫時,比熱隨溫度下降而減少,必須應用量子理論解釋 晶格振動能, U=(i+½)ℎν, i=1, 2, … 在0 K晶格振動能為½ℎν, 加熱至T K,增加n個能量子ℎν ,使它們分布至N個原子的三維晶體中(3N個振子因為每個原子有3個自由度)讓亂度增加,即熵增加→ 利用自由能A=U-TS 在T K時吸收nℎν達熱平衡: dA/dn=dU/dn-T(dS/dn)=0 U=U₀+nℎν, U₀是0 K時的能量,所以 dU/dn=ℎν
⸫ ℎν=kTln[(n+3N)/n] → Cᵥᵃ=dU/dT=d(U₀+nℎν)/dT=d[3Nℎν/(eℎν/kT-1)]/dT=3Nk(ℎν/kT)²eℎν/kT /(eℎν/kT-1)² 令θᴇ=ℎν/k, Cᵥᵃ=3R(θᴇ/T)²eθᴇ/T/(eθᴇ/T-1)²
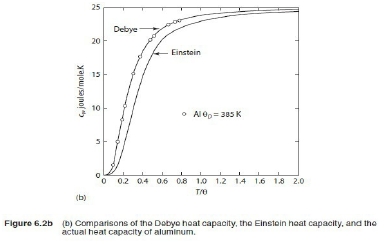
(1)在0 K, Cᵥᵃ=0, (2)高溫時 ℎν/kT<<1 span="">, 使得eℎν/kT≈1+ ℎν/kT, Cᵥᵃ=3Nk(ℎν/kT)²(1+ ℎν/kT)/(ℎν/kT)² ≈3R (3)極低溫時ℎν/kT>>1, Cᵥᵃ=3R(ℎν/kT)²e-ℎν/kT 比實驗值更快趨近於零, 所以Debye將振動頻率的差別考慮放入Cᵥᵃ=d[3Nℎν/(eℎν/kT-1)]/dT, 改寫為:
Planck distribution, n=1/(eℏω/kT-1) define →
在3-D的k空間,每一個能態佔有體積(2π/L)³, 所有能態數目=(4πk³/3)/(2π/L)³=Vk³/6π²=n(k) 能態密度D(k): dn(k)=n(k+dk)-n(k)=(dn/dk)∙dk= (Vk²/2π²)∙dk=D(k)∙dk, ⸫ D(k)=Vk²/2π² 變數置換k→ω, 因為設定波速υ 固定 υ=ω/k, dω=υdk D(k)∙dk=(Vk²/2π²)∙dk=(Vω²/2π²υ²)(dω/υ)=(Vω²/2π²υ³)dω 假設晶體有N個原子,即有N個聲子能態,每個聲子有3種極化波速3/υ³=1/υₗ³+1/υₜ₁³+1/υₜ₂³) 總能量
N=n(k)=Vk³/6π² → n(ωᴅ)=N=Vωᴅ³/6π²υ³ ⸫ ωᴅ³= 6π²υ³N/V, and ℏωᴅ/kT=θᴅ/T Cᵥᵃ=dU/dT=
⸫ Cᵥᵃ=3R∙fᴅ(θᴅ/T), (1) 高溫時 ℏωᴅ/kT=xᴅ=θᴅ/T<<1, e="" font="">x=1+x+x²/2!+x³/3!+... 當x<<1 font="">
→ Cᵥᵃ=dU/dT=3R (2)極低溫時 ℏωᴅ/kT=xᴅ=θᴅ/T→∞, 1/(ex-1)=e⁻x/(1-e⁻x)=e⁻x+e⁻²x+e⁻³x+...= ⸪ → Cᵥᵃ=dU/dT=(12π⁴R/5)(T/θᴅ)³~T³, T³ law 與電子比熱 Cᵥ=Cᵥᵃ+Cₑₗ=γT+bT³ or Cᵥ/T=γ+bT² 作圖求γ, b 一般溫度下, 電子比熱Cₑₗ的佔比很小,需要考慮的情形: (1)極低溫度時, (2)過渡元素因為ns, (n-1)d能帶重疊,而且d能帶密度很高,所以Cₑₗ比一般金屬大得多 振動熵Sυ, Sυ=kln[(n+3N)!/n!3N!]=k[(n+3N)ln(n+3N)-nlnn-3Nln3N] ⸪ n=3N/(ehν/kT-1) 且 hν/kT→0, let ehν/kT≈1+ hν/kT ⸫ n≈3N/(hν/kT)代入Sυ 令hν/kT=t, Sυ=k[(n+3N)ln(n+3N)-nlnn-3Nln3N]=k[3N(1+t⁻¹)ln3N(1+t⁻¹)-(3N/t)ln(3N/t)-3Nln3N] =3Nk[(1+t⁻¹)ln(1+t⁻¹)-t⁻¹lnt⁻¹]=3R[ln(1+t⁻¹)+t⁻¹ln(t+1)]=3R[ln(1+kT/hν)+(kT/hν)ln(hν/kT+1)] i.e. ln(hν/kT+1)≈hν/kT-½(hν/kT)² → Sυ=3R[(1-hν/2kT)+ln(1+kT/hν)] at high temp., hν/kT<<1 i="">Sυ=3R[1+ln(kT/hν)] if frequency changed, ν → ν, ∆Sυ=Sν-Sν=3Rln(ν/ν)>0 if ν>ν 多形性轉變 微觀的振動原子看成彈簧的簡諧運動, F=-αy, y: 位移同時原子間距=a, 將其改寫為應力-應變形式(σ=Eε) → F/a²=-E(y/a) ⸫ α=aE i.e. E為彈性模數,Youngs modulus 簡諧振動頻率ν=(1/2π)(α/m)½=(1/2π)(aE/m)½ 根據原子鍵結的能勢圖,鍵結能(力)越大,其E值也越大,振動頻率ν隨E增加
由前面比熱公式推導得知, Cᵥᵃ=(12π⁴R/5)(T/θᴅ)³, θᴅ=ℎνₘ/k稱為Debye溫度, 振動頻率ν大則θᴅ 大,比熱就變小 ex. gray Sn →加熱→ white Sn ∆G=∆H-T∆Sυ 自發反應的∆G<0, font="">因為∆H>0(吸熱),所以∆Sυ>0 可知νgray>νwhite, ⸪ ∆Sυ=3Rln(νgray/νwhite)>0 判斷反應如何進行? 必須同時考慮∆H與∆S,兩者的綜合表現即是∆G,此例可以看出∆H與∆S是同號,高溫時從灰錫變白錫,-T∆S起主要作用使∆G<0; font="">反之,降溫時∆H影響變大使∆G>0,變成灰錫. G-T圖顯示Tc以下,灰錫的自由能小於白錫,所以灰錫穩定;反之,Tc以上白錫為穩定相 自由能曲線交叉的原因 晶體在恆壓下加熱, T→T+dT G=H-TS, dG=dH-TdS-SdT=CₚdT-T∙(CₚdT/T)-SdT=-SdT i.e. dH=dQ=CₚdT, dS=δQ/T=CₚdT/T →積分 G-G₀=∫₀ᵀ-SdT, G=H₀-∫₀ᵀ(∫₀ᵀCₚdT/T )dT i.e. G₀為0K時的自由能, G₀= H₀ 從式中看出,升溫時G會減少,比熱越大降得越快,所以白錫在高溫為穩定相可推得其比熱較大,進一步得到其θᴅ 較小, νwhite也較小,E和鍵結能也比灰錫小 例外: Fe的相轉變, α-Fe→910℃→γ-Fe→1400℃→δ-Fe→1539℃→liquid Fe 主要因子根據(1)比熱vs.溫度關係圖, (2)過渡金屬的電子比熱較大
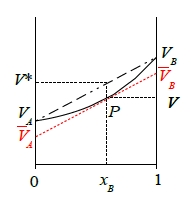
因為θα>θγ的緣故, γ-Fe的比熱較大,促使α→γ在910℃發生;另外α-Fe的電子比熱在300℃以上大於γ-Fe,使γ→δ在1400℃發生 比熱曲線與相轉變, p.119 Smallman 若金屬在固定溫度進行1st order相轉變, ex. α→γ, γ→δ 比熱曲線會產生不連續(因為潛熱吸收部會造成溫度變化, dQ/dT→∞), 若是2nd order相轉變, ex. 鐵磁→順磁(有序到無序過程)發生在一溫度範圍,範圍越窄,峰值越尖,極端的情形極逼近1st order相轉變 p.126: 從比熱性質探討自由能變化與相變化的關係, G=H₀-∫₀ᵀ(∫₀ᵀCₚdT/T )dT 低溫時,有關比熱的∫₀ᵀ(∫₀ᵀCₚdT/T )dT對自由能不重要,主要在於H₀的大小, H₀越小的相在低溫時越穩定;相對而言,比熱大的相在高溫時,自由能下降較快,相對穩定.所以低溫時比熱小的強鍵結力的緊密堆積結構比較穩定,而高溫時比熱大的弱鍵結疏鬆結構則相對穩定,也符合隨溫度升高,固體變成液體的現象 在鐵的特例中,低溫的bcc結構(α-Fe),其原子間距允許電子採平行自旋的排列,達到內能與熵最小的狀況. 升溫時飽和磁化開始下降逐漸加快,直到居禮點鐵磁變成順磁,因為熱擾動破壞d電子的自旋平行排列,使這種無序產生的熵增加, ex. N個自旋平行的電子中,n個因熱擾動變成反平行; 增加的磁熵∆S=kln[N!/n!(N-n)!], 電子交換作用也使內能增加,其增量對溫度也貢獻附加比熱,同時磁熵與附加比熱對γ→δ也有影響 Molar quantity: 研究某成分在固溶體中的熱力性質 ex. molar volume, Vᵢ : 由1, 2,...,i,..個成分組成的固溶體,其體積V隨成分而變, V=f(n₁,n₂,..nᵢ,..) 假設在恆溫恆壓下,增加微量dnᵢ, 體積的變化為 dV=(∂V/∂n₁)T,P,n₂,n₃,...dn₁+(∂V/∂n₂)T,P,n₁,n₃,...dn₂+... define Vᵢ=(∂V/∂nᵢ)T,P,nj,... 因此dV=V₁dn₁+V₂dn₂+... (1), 當成分一定時,→積分 V=V₁∫₀ₙ₁dn₁+V₂∫₀ₙ₂dn₂+...=V₁n₁+V₂n₂+... ⸫ V=V₁n₁+V₂n₂+... 微分得 dV=V₁dn₁+n₁dV₁+V₂dn₂+n₂dV₂+... (2) 與(1)比較得 n₁dV₁+n₂dV₂+...=0 Gibbs-Duhem eq. Gibbs-Duhem eq.在熱力學的狀態函數都可適用, ex. U, H, A, G, S...
理想固溶體的體積V*, V*=VAxA+VBxB 是純元素體積VA,VB的線性組合 一般固溶體為非理想固溶體,它的體積V, V=VAxA+VBxB 可視為成分曲線在P點的線性組合 VA,VB可改寫成 VA=V-xB(dV/dxB), VB=V+(1-xB)(dV/dxB) 多相平衡的化學勢,μᵢ 如同體積,自由能變化可表示為 dG=(∂G/∂T)P,nᵢ,...dT+(∂G/∂P)T,nᵢ,...dP+(∂G/∂n₁)T,P,n₂,n₃,...dn₁+(∂G/∂n₂)T,P,n₁,n₃,...dn₂+... → (∂G/∂T)P,nᵢ,...=-S, (∂G/∂P)T,nᵢ,...=V, (∂G/∂n₁)T,P,n₂,n₃,...=G₁, (∂G/∂n₂)T,P,n₁,n₃,...=G₂... G₁, G₂分別為成分1, 2,...,i,..的molar free energy, 也可稱為化學勢, Gᵢ=μᵢ ⸫dG=-SdT+VdP+G₁dn₁+G₂dn₂+...=-SdT+VdP+μ₁dn₁+μ₂dn₂+...若在恆溫恆壓下,dG=μ₁dn₁+μ₂dn₂+... 同理dG也遵守Gibbs-Duhem eq. n₁dμ₁+n₂dμ₂+...=0 當G=μ₁n₁+μ₂n₂+... 求i成分的化學勢: 固溶體來自溶液理論,溶液理論又來自混合氣體, 理想混合氣體方程式PV=RT, 對單原子分子,i成分的分壓Pᵢ=Pxᵢ=RTxᵢ/V → V=RTxᵢ/Pᵢ, xᵢ=nᵢ/(n₁+n₂+..+nᵢ+...) if n₁+n₂+..+nᵢ+...=1, V=RTnᵢ/Pᵢ → 對nᵢ微分Vᵢ=∂V/∂nᵢ=RT/Pᵢ and (∂G/∂P)T,nᵢ,...=V → Vᵢ=∂[(∂G/∂P)T,nᵢ,...]/∂nᵢ=∂[∂G/∂nᵢ]/∂P|T,nᵢ,...=(∂μᵢ/∂P)T,nᵢ,... ⸫ Vᵢ=∂μᵢ/∂P → dμᵢ=VᵢdP=RTdP/Pᵢ →積分 μᵢ=∫₀PᵢRTdP/Pᵢ =μᵢ⁰(T)+RTlnPᵢ 討論A,B二元系統中α,β兩相在恆溫恆壓下的平衡, α,β兩相分別有自由能:
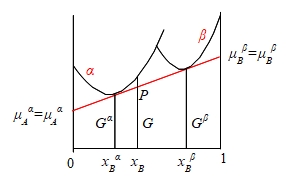
Gα=μAαxAα+μBαxBα, Gβ=μAβxAβ+μBβxBβ 設想一微量dnA從α相移到β相,系統自由能變化:
dG=dGα+dGβ=-μAαdnA+μAβdnA=(μAβ-μAα)dnA 平衡狀態下,dG=0 ⸫ μAβ=μAα同理 μBβ=μBα
推廣至多元系統(1,2,...,i,..)的多相(α,β,γ,...)平衡條件: μᵢα=μᵢβ=μᵢγ=... i=1, 2,...
即在恆溫恆壓下任一成分在各相中的化學勢相等;換句話,如果任一成分在兩相中的化學勢不相等,它會從化學勢高的相流動到化學勢低的相,使系統的自由能降低,直到兩相的化學勢相等為止,所以化學勢的梯度是固溶體中物質流動的驅動力
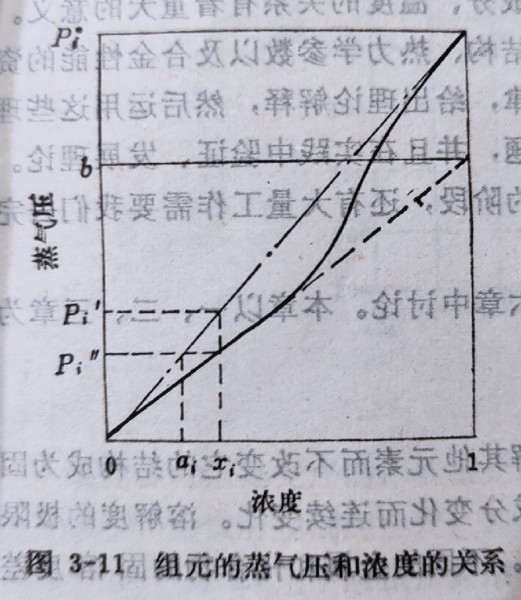
活性activity 理想溶液中蒸氣壓Pᵢ與濃度xᵢ有線性關係, Pᵢ=xᵢPᵢ*...Raoults law Pᵢ*: 純i的蒸氣壓 代入μᵢ=μᵢ⁰(T)+RTlnPᵢ → μᵢ=μᵢ⁰(T)+RTln(xᵢPᵢ*)=μᵢ⁰(T)+RTlnPᵢ*+RTlnxᵢ=μᵢ⁰(T,P)+RTlnxᵢ 若是非理想溶液的蒸氣壓, Pᵢ=aᵢPᵢ* aᵢ稱為i成分的活性 同樣代入μᵢ, μᵢ=μᵢ⁰(T,P)+RTlnaᵢ 實驗指出,當濃度xᵢ →0(稀薄),Pᵢ與濃度xᵢ也有線性關係, Pᵢ=bxᵢ...Henrys law
aᵢ=Pᵢ/Pᵢ*=bxᵢ/Pᵢ*=γᵢxᵢ, i.e. γᵢ=b/Pᵢ* γᵢ 稱為活性係數 → μᵢ=μᵢ⁰(T,P)+RTlnaᵢ=μᵢ⁰(T,P)+RTlnxᵢ+RTlnγᵢ 非理想溶液的化學勢只需與假想的理想溶液比較,取決於非理想項RTlnγᵢ的差距
|
|
| ( 知識學習|科學百科 ) |




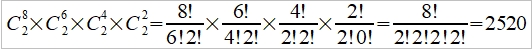
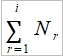
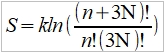
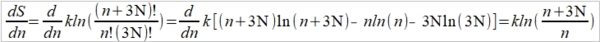
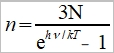
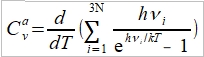
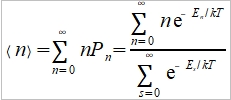
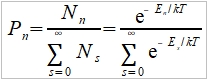
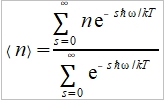 令
令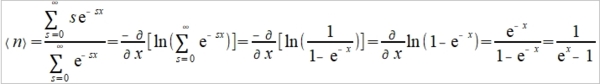
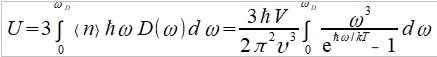 令
令