微觀系統的動態: 以物質波作為出發點,放棄古典的粒子軌跡概念,將粒子的位置看成像波的振幅分佈一樣;波函數取代軌跡,於是建立一套如何計算和解釋波函數的力學

薛丁格方程式是一種卓越的假設,它的解就是波函數: ex. (-ℏ²/2m)(d²ψ/dx²)+Vψ=Eψ描述質量m的粒子有能量E在x方向上運動,V是粒子的位能,與位置有關

若考慮V=0,自由電子的運動 (-ℏ²/2m)(d²ψ/dx²)=Eψ, 其解ψ=e^ikx=coskx+isinkx, k=(2mE/ℏ²)^½

since k=2π/λ, and E=ℏ²k²/2m, ⸫ p=ℏk=(h/2π)(2π/λ)=h/λ 得到de Broglie relation

當位能均勻分布,即V=V₀(常數)時,方程式為(-ℏ²/2m)(d²ψ/dx²)=(E-V₀)ψ,其解不變,但k=[2m(E-V₀)/ℏ²]^½→動能=E-V₀=ℏ²k²/2m, and λ=h/p=h/[2m(E-V₀)]^½ 顯示動能越大,波長就越短;譬如靜止的粒子,其波長無限大,表示波函數在任何地方都一樣, ψ= 常數.另外觀察方程式,動能變大使 d²ψ/dx²也增加,d²ψ/dx²代表波函數的曲率curvature, 即曲率變大,符合波長變短的波形

薛丁格方程式是二次微分方程式,可以有無窮解,例如: ψ=e^-ikx, Ae^-ikx 也是,k也可以任意值,但是許多數學上的解在物理是不可允許的,剔除這些解意味有些能量值被排除,能量量子化的意義出現了!

薛丁格方程式: 一維系統, (-ℏ²/2m)(d²ψ/dx²)+Vψ=Eψ or d²ψ/dx²+(2m/ℏ²)(E-V)ψ=0, V=V(x), ψ=ψ(x) i.e. V是粒子的位能, ex. V=0 for a free particle, V=½kx² for a harmonic oscillator.

三維系統, (-ℏ²/2m)²ψ+Vψ=Eψ, V=V(x,y,z), ψ=ψ(x,y,z) where ²=(∂²/∂x²)+(∂²/∂y²)+(∂²/∂z²)

若是球座標. ²=(∂²/∂r²)+(2/r)(∂/∂r)+(1/r²)Λ², Λ²=(1/sin²θ)(∂²/∂ϕ²)+(1/sinθ)(∂/∂θ)sinθ(∂/∂θ)

一般的表示: Hψ=Eψ, where hamiltonian operator, H=(-ℏ²/2m)²+V

如果是時變薛丁格方程式: Hψ=iℏ(∂ψ/∂t)

波函數的意義: Born用光波的理論來解釋,電磁波的振幅平方代表光的強度,或是光子的數量;波函數的平方ψ^*ψ即代表空間中某處找到粒子的機率密度; P=ψ^*ψdx

在三維空間, ex. 原子核附近的電子, 它的波函數ψ(r), 該點r的機率=ψ^*ψdτ, dτ=dxdydz

ex. 氫原子的電子,其最低能態的波函數ψ(r)e^-r/a₀, a₀=52.9 pm, 計算發現電子在體積1 pm³位於(1)原子核, (2)距離a₀ 的相對機率

(1)r=0, ψ^*ψ1, ψ^*ψdτ1.0 (2)r=a₀, ψ^*ψdτe^-²1.0=0.135 相對機率=1/0.135=7.1

歸一化常數, N: 因為波函數解有無窮多,利用機率分佈的積分找出歸一化的波函數

N²∫_-∞^∞ψ^*ψdx=1, or N²=1/∫_-∞^∞ψ^*ψdx; A∫_-∞^∞ψ^*ψdxdydz=1 for 3-D

ex. 氫原子的電子波函數ψ(r)e^-r/a₀, 找出歸一化的波函數

ψ(r)=Ne^-r/a₀, ∫_-∞^∞ψ^*ψdτ=N²∫₀^∞r²e^-²^r/a₀dr∫₀^πsinθdθ∫₀^2πdϕ i.e. x=rsinθcosϕ, y=rsinθsinϕ, z=rcosθ, dτ=r²drsinθdθdϕ, ⸫ ∫_-∞^∞ψ^*ψdτ=N²(a₀³/4)∙2∙2π=πa₀³N²=1, ψ(r)=Ne^-r/a₀=(1/πa₀³)^½e^-r/a₀

p.s. ∫₀^∞ xⁿe^-axdx=n!/aⁿ⁺¹

波函數的限制: a. 連續的 b. 斜率是連續的 c. 單一數值 d. 有限收斂

算子與可觀察量: 薛丁格方程式的一般表示: Hψ=Eψ, with H=(-ℏ²/2m)²+V 有eigenvalue equation特徵值方程式的形式: (operator)(function)=(numerical factor)(same function), 意即數值因子是算子的特徵值,函數則是相應於特徵值的特徵函數eigenfunction ;所以薛丁格一般式中,能量E是算子H的特徵值,波函數是能量E的特徵函數

ex. is cosax an eigenfunction of (a)d/dx, (b)d²/dx²?

(a)Ô=d/dx and f=cosax, Ôf=(d/dx)cosax=-a(sinax) No!

(b)Ô=d²/dx² and f=cosax, Ôf=(d²/dx²)cosax=-a²(cosax) Yes!

因此薛丁格方程式的形式可看成: (operator)(wavefunction)=(observable)(wavefunction)

Ôψ=Oψ

以自由電子的波函數ψ=Ae^ikx+Be^-ikx, if B=0, dψ/dx=ikψ兩邊同乘(ℏ/i), (ℏ/i)dψ/dx=ℏkψ

⸪ p=ℏk, (ℏ/i)d/dx(ψ)=pψ, ⸫ Ṕ=(ℏ/i)d/dx=-iℏ(d/dx)

若含時間變數,ψ=Ae^i(kx-ωt), dψ/dt=-iωψ兩邊同乘(-ℏ/i), (-ℏ/i)dψ/dt=ℏωψ

⸪ E=ℏω, (-ℏ/i)d/dt(ψ)=ℏωψ, ⸫ Ȇ=(-ℏ/i)d/dt=iℏ(d/dt)

將算子代入(p²/2m+V)ψ=Eψ, Ṕ²ψ/2m+Vψ=Ȇψ

→ -ℏ²/2m(d²ψ/dx²)+Vψ=iℏ(dψ/dt), H=(-ℏ²/2m)(d²/dx²)+V → 時變薛丁格方程式: Hψ=iℏ(∂ψ/∂t)

疊加原理與期望值:

自由電子的波函數ψ=Ae^ikx+Be^-ikx, 假設A=B, ψ=A(e^ikx+e^-ikx)=2Acoskx, 如果用Ṕ操作

-iℏ(d/dx)2Acoskx= iℏk(2Asinkx)發現不是eigenvalue equation,告訴我們動量是不確定的,是由於cosine波函數是e^ikx和e^-ikx的加總,每個波都有相應的動量,可以寫成疊加: ψ=ψ(○→)+ψ(←○)

所以波函數可以是許多不同動量的特徵波函數的組合: ψ=c₁ψₚ₁+c₂ψₚ₂+...

其特性有:1.唯有在疊加中的特徵波函數,才能找到相應的特徵值 2.無法預測會發現哪個可能值 3.在一串的觀測中測得其中的特徵值的機率,與其係數平方cᵢ^*cᵢ成正比 4.大量觀察的平均值即是可觀察量的期望值O

O=∫ψ^*Ôψdτ, ψ: 歸一化的波函數, Ô: 特徵值的算子

ex. 計算電子離氫原子核的平均距離

r=∫ψ^*rψdτ, ψ=(1/πa₀³)^½e^-r/a₀,

r=(1/πa₀³)∫₀^∞r³e^-²^r/a₀dr∫₀^πsinθdθ∫₀^2πdϕ=(1/πa₀³)∙3!∙(2/a₀)⁻⁴∙2∙2π=3a₀/2=79 pm

ex. evaluate the root mean square distance, rᵣₘₛ=r²^½

r²=(1/πa₀³)∫₀^∞r⁴e^-²^r/a₀dr∫₀^πsinθdθ∫₀^2πdϕ=(1/πa₀³)∙4!∙(2/a₀)⁻⁵∙2∙2π=3a₀², rᵣₘₛ=√3a₀=102.5 pm

測不準原則: 如果粒子的波函數是Ae^ikx, 經過算子運算可知動量為ℏk, 但是粒子的位置在哪?必須由機率密度ψ^*ψ得知, ψ^*ψ=Ae^-ikxAe^ikx=A²,表示到處發現粒子的機率相同;換言之,如果精確得知動量,就不可能知道粒子的位置

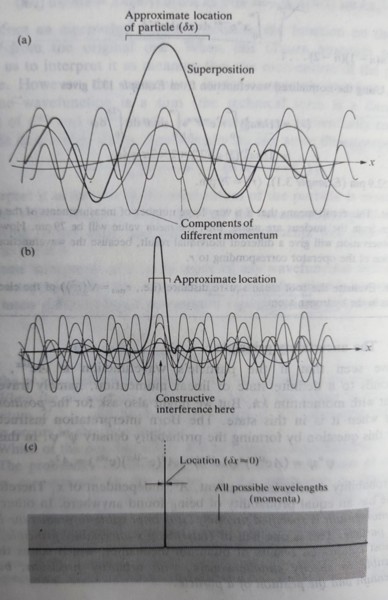
假設我們知道粒子的確實位置,同時已知粒子的波函數是由不同動量的特徵函數所疊加的狀態,因此可以創造非常完美、小範圍的波函數去確定粒子的位置,但波函數會包含即大量的動量特徵值疊加在一起, 造成動量不可測! 海森堡考慮位置與動量的期望值,提出一定量關係

δpδx≥ℏ/2, where δx=xᵣₘₛ-x, δp=pᵣₘₛ-p

ex. estimate the minimum uncertainty in the speed of an electron in a H atom.

Taking its diameter as 2a₀=105.8 pm, δp=mₑδv≥(ℏ/2)/δx=(1.055∙10⁻³⁴/2)/105.8∙10⁻¹²=4.98∙10⁻²⁵

δv≥4.98∙10⁻²⁵/9.10953∙10⁻³¹=547 kms⁻¹

海森堡關係應用於許多配對的互補可觀察量,如位置與動量,時間與能量..., 此時,我們已站在古典與量子物理的差異上! 古典物理的例子都能預測準確的軌跡,而且控制施力就可得任何的能量,但是當處理非常小的質點或能量時,變得無法同時得知x與p描述粒子的軌跡,能量傳遞也不是連續的

第14章 量子理論應用與技術

三種運動:平移,振動,旋轉;是分子儲能的重要方式,牽涉到動能以及能階間遷移所產生的旋轉和振動光譜

1. 平移運動: 量子力學用薛丁格方程式描述自由運動, (-ℏ²/2m)(d²ψ/dx²)=Eψ, ψ=Ae^ikx+Be^-ikx, k=(2mE/ℏ²)^½ 若B=0,波函數代表粒子帶有ℏk動量往右運動;反之,若A=0,粒子往左,此時粒子能量還未量子化,假設粒子的自由範圍被限制在x=0~L的位能井中,井中V=0而其餘V=∞

當0<x粒子的運動如自由運動: (-ℏ²/2m)(d²ψ/dx²)=Eψ, ψ=Asinkx+Bcoskx, k=(2mE/ℏ²)^½ (14.1)

現在考慮x<0 span="">和x>L時, (-ℏ²/2m)(d²ψ/dx²)+Vψ=Eψ or d²ψ/dx²=(2m/ℏ²)(V-E)ψ (14.2)觀察方程式,因為V>>E,若ψ>0, d²ψ/dx²>0表示曲率遞增,波形為︶;若ψ<0, d²ψ/dx²<0 span="">表示曲率遞減,波形為︵,但無論ψ的正負,V=∞都會使d²ψ/dx²發散,均不被接受,因此唯有ψ=0可允許,於是乎在x=0和x=L出現邊界條件:ψ(0)=ψ(L)=0.

(14.2)的解: ψ=Ae^kx+Be^-kx, k=[2m(V-E)/ℏ²]^½ let A=0使ψ不發散, ψ=Be^-kx,V=∞也使ψ(0),ψ(L)很快歸零,符合邊界條件的要求

(14.1)的解: ψ=Asinkx+Bcoskx也需符合邊界條件:ψ(0)=ψ(L)=0, ψ(0)=B ⸫B=0, ψ=Asinkx; ψ(L)=AsinkL=0 → sinkL=0 ⸫ kL=nπ, n=1,2,3...

粒子能量受限,E=n²ℏ²π²/2mL²=n²h²/8mL² n=1,2,3... 量子化

歸一化波函數: 1=∫₀^Lψ^*ψdx=A²∫₀^Lsin²kxdx=A²L/2, A=(2/L)^½

(14.1)的完整解: ψₙ=(2/L)^½sin(nπx/L), Eₙ=n²h²/8mL² n=1,2,3...

(14.1)的完整解: ψₙ=(2/L)^½sin(nπx/L), Eₙ=n²h²/8mL² n=1,2,3...

解的性質: 粒子波函數的形狀如駐波,為了符合方井,連續的波函數都有半波長的整數倍,波長縮短意即波函數的曲率提高,粒子的動能也增加,但動量無法從sinkx駐波由算子得到,因為駐波不是動量的特徵函數,每個駐波都是動量的特徵函數的疊加態; sinkx=(e^ikx-e^-ikx)/2i→ψ₁=e^ikx/2i, ψ₂=-e^-ikx/2i, Ṕψ₁=ℏk(e^ikx/2i)=ℏkψ₁ and Ṕψ₂=ℏk(-e^-ikx/2i)=-ℏkψ₂ ⸪ Ṕ=-iℏ(d/dx),特徵值ℏk=(h/2π)(nπ/L)=nh/2L一半往右(ℏk)和一半往左(-ℏk)

因為n≠0,粒子在井內的最低能量E₁=h²/8mL²(稱零點能量),從測不準原則看粒子,雖然侷限在井中,但不完全確定位置,所以動量不會為零,存在動能;另外,波函數除了在井壁為零,其他地方都是平滑連續不為零的曲線,他的曲率代表粒子擁有動能

相鄰能階的能量: ∆E=Eₙ₊₁-Eₙ=(2n+1)h²/8mL² 當井的邊長L增加,∆E開始減小,若L→∞, ∆E→0粒子的能量量子化也就消失

粒子在井中的分布並不均勻,其在x的機率: (2/L)sin²(nπx/L),當n越小時,分布不均勻的現象越明顯;反之,量子數越大,粒子的分布機率越均勻,使古典力學與量子力學可以相容

二維運動: 當粒子在四方井中(L₁L₂), V=0(出了方井,V=∞), 薛丁格方程式:

(-ℏ²/2m){(∂²ψ/∂x²)+(∂²ψ/∂y²)}=Eψ, 採分離變數法, set ψ(x,y)=X(x)Y(y)

(-ℏ²/2m){(∂²XY/∂x²)+(∂²XY/∂y²)}=EXY→ (-ℏ²/2m){(X"/X)+(Y"/Y)}=E

→ (-ℏ²/2m)(X"/X)=E^X, (-ℏ²/2m)(Y"/Y)=E^Y with E^X+E^Y=E

Xₙ₁=(2/L₁)^½sin(n₁πx/L₁), Yₙ₂=(2/L₂)^½sin(n₂πy/L₂), since ψ(x,y)=X(x)Y(y)

ψₙ₁_,ₙ₂=(4/L₁L₂)^½sin(n₁πx/L₁)sin(n₂πy/L₂) (14.3), Eₙ₁_,ₙ₂=E^Xₙ₁+E^Yₙ₂={(n₁/L₁)²+(n₂/L₂)²}h²/8m (14.4), n₁=1,2,3..., n₂=1,2,3...

若L₁=L₂=L, ψₙ₁_,ₙ₂=(2/L)sin(n₁πx/L)sin(n₂πy/L), Eₙ₁_,ₙ₂={(n₁²+n₂²}h²/8mL²

ex. 考慮n₁=1, n₂=2 and n₁=2, n₂=1

ψ₁_,₂=(2/L)sin(πx/L)sin(2πy/L), E₁_,₂=5h²/8mL², ψ₂_,₁=(2/L)sin(2πx/L)sin(πy/L), E₂_,₁=5h²/8mL²

注意:不同的波函數相應於一樣的能量,這是簡併的條件,簡併的發生是有關系統的對稱,因為L₁=L₂=L, 旋轉平面90°即對稱(如圖14.4)

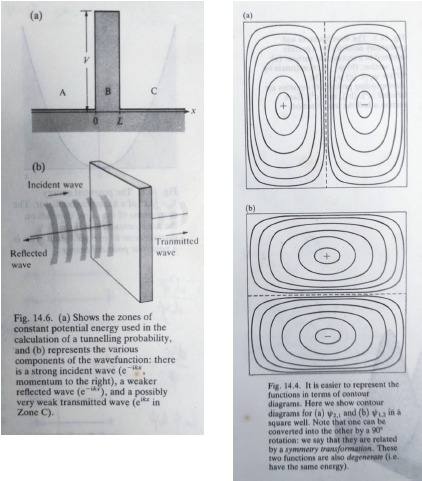
量子洩漏: 若粒子處於的位能井,其井壁並非無限高,此條件會使波函數在井壁處發生非零的情況,假如位能壁很薄,使的波函數衰退停止,重新開始像井內振盪一樣;這意味粒子可以在井外被發現,即使它的能量不足以跳脫,此種洩漏稱作隧道效應Tunnelling. 從方程式計算隧道效應的程度,發現輕的粒子比較容易穿隧能障,所以對電子很重要

ex. 一電子從左入射,中間有位能障V(0<x電子動能E<V, 如圖14.6(a)所示

每區的薛丁格方程式:

A區 (-ℏ²/2m)(d²ψ/dx²)=Eψ, ψ_A=Ae^ikx+Ae^-ikx, k=(2mE/ℏ²)^½

B區 (-ℏ²/2m)(d²ψ/dx²)+Vψ=Eψ, ψ_B=Be^κx+Be^-κx, κ=[2m(V-E)/ℏ²]^½

C區 (-ℏ²/2m)(d²ψ/dx²)=Eψ, ψ_C=Ce^ikx+Ce^-ikx, k=(2mE/ℏ²)^½ i.e. C=0 因為沒有反射波

每區之間的邊界,波函數及其導數必須符合連續的條件,所以ψ_A(0)=ψ_B(0), ψ_A(0)=ψ_B(0) and ψ_C(L)=ψ_B(L), ψ_C(L)=ψ_B(L)將邊界條件代入波函數解中,可得4個條件式:

A+A=B+B (i), ikA-ikA=κB-κB (ii), Be^κL+Be^-κL=Ce^ikL (iii), κBe^κL-κBe^-κL=ikCe^ikL (iv),

利用(i)(ii)捨去A, 2ikA=(ik+κ)B+(ik-κ)B →2A=(1-iκ/k)B+(1+iκ/k)B (v)

利用(iii)(iv), 2κBe^-κL=κCe^ikL-ikCe^ikL → 2Be^-κL=(1-ik/κ)Ce^ikL (vi), 2Be^κL=(1+ik/κ)Ce^ikL (vii)

將(vi)(vii)代入(v), 2A=[(1-iκ/k)e^-κL(1+ik/κ)+(1+iκ/k)e^κL(1-ik/κ)]Ce^ikL/2 (viii)

→ (1-iκ/k)e^-κL(1+ik/κ)+(1+iκ/k)e^κL(1-ik/κ)=[(2+ik/κ-iκ/k)e^-κL+(2-ik/κ+iκ/k)e^κL]=2(e^κL+e^-κL)+i(k/κ-κ/k)e^-κL+i(κ/k-k/κ)e^κL= 2(e^κL+e^-κL)+i(κ²-k²)(e^κL-e^-κL)/κk 代回(viii)

→ A=[(e^κL+e^-κL)/2+i(κ²-k²)(e^κL-e^-κL)/4κk]Ce^ikL (viiii), 我們可以計算穿透率估計隧道效應Tunnelling.

穿透率, P=|C|²/|A|², since (viiii), A/C=[(e^κL+e^-κL)/2+i(κ²-k²)(e^κL-e^-κL)/4κk]e^ikL

⸫ P⁻¹=|A/C|²=|(A/C)(A/C)^*|=|[(e^κL+e^-κL)/2+i(κ²-k²)(e^κL-e^-κL)/4κk]e^ikL∙[(e^κL+e^-κL)/2-i(κ²-k²)(e^κL-e^-κL)/4κk]e^-ikL|=|(e^κL+e^-κL)²/4+[(κ²-k²)/4κk]²(e^κL-e^-κL)²| (x)

where cosh²x=1+sinh²x, (e^κL+e^-κL)²/4=1+(e^κL-e^-κL)²/4 (xi), and since

k=(2mE/ℏ²)^½, κ=[2m(V-E)/ℏ²]^½ → [(κ²-k²)/4κk]²={(2m(V-E)/ℏ²-2mE/ℏ²)/[4(2mE/ℏ²)^½[2m(V-E)/ℏ²]^½]}²

=(V-2E)²/[16E(V-E)]=V²(1-2ε)²/[16V²ε(1-ε)]=(1-2ε)²/[16ε(1-ε)] (xii) i.e. ε=E/V

將(xi)(xii)代入(x), P⁻¹=|1+(e^κL-e^-κL)²/4+(1-2ε)²(e^κL-e^-κL)²/[16ε(1-ε)]|=|1+{1+(1-2ε)²/[4ε(1-ε)]}(e^κL-e^-κL)²/4|=|1+(e^κL-e^-κL)²/[16ε(1-ε)]|=|1+G|, where G=(e^κL-e^-κL)²/[16ε(1-ε)]

穿透率, P=1/|1+G|, where G=(e^κL-e^-κL)²/[16ε(1-ε)], ε=E/V

若能障很大且厚(L很大), κL>>1即e^κL>>e^-κL ,所以G>>1, P≈[16ε(1-ε)]/e²^κL

2. 振動: 舉粒子進行簡諧運動,受恢復力在平衡位置前後位移, F=-kx;所以好似一束縛電子受原子核的位能井約束做振動,因此簡化為簡諧運動,其位能V=-∫Fdx=½kx²隨x²遞增

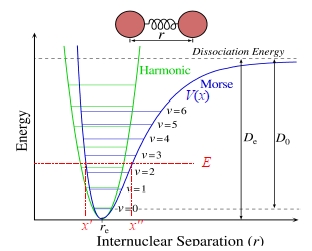
簡諧運動的薛丁格方程式: (-ℏ²/2m)(d²ψ/dx²)+½kx²ψ=Eψ or d²ψ/dx²=(mk/ℏ²)x²ψ-(2mE/ℏ²)ψ (14.5), 先以變數變換簡化方程式

set y=x/α, α²=ℏ/(mk)^½ and ε=E/(½ℏω), ω=(k/m)^½ 代入(14.5)

dψ/dx=(dψ/dy)(dy/dx)=(1/α)dψ/dy, d²ψ/dx²=d/dx(dψ/dx)=(1/α)d/dx(dψ/dy)=(1/α)d/dy(dψ/dy)dy/dx=(1/α²)d²ψ/dy²

→ (1/α²)d²ψ/dy²=(x²/α⁴)ψ-(mωε/ℏ)ψ=(y²/α²)ψ-(m^½ k^½ ε/ℏ)ψ=(y²/α²)ψ-εψ/α²→ d²ψ/dy²=(y²-ε)ψ (14.6)

若x→∞(y→∞), y²>>ε to let d²ψ/dy²=y²ψ, ψ=Ae^y²/2+Be^-y²/2, 所以A=0(當y→∞)才不會發散, ψ=Be^-y²/2與方井的波函數e^ikx相比,e^-y²/2收斂更快是因為位能½kx²隨x²遞增,波函數也就遞減更快

令ψ=f(y)e^-y²/2代入(14.6), dψ/dy=fe^-y²/2-yfe^-y²/2, d²ψ/dy²=[f"-2yf+(y²-1)f]e^-y²/2,

→ [f"-2yf+(y²-1)f]e^-y²/2+(ε-y²)fe^-y²/2=0→ [f"-2yf+(ε-1)f]e^-y²/2=0 ⸫ f"-2yf+(ε-1)f=0 Hermites eq.(14.7)

(14.7)用冪級數法求解: 設f(y)=∑ₖ₌₀^∞aₖy^k=a₀+a₁y+a₂y²+...

f(y)=a₁+2a₂y+3a₃y²+...+kaₖy^k-1+(k+1)aₖ₊₁y^k+... ,

f"(y)=2a₂+6a₃y+12a₄y²+...+k(k+1)aₖ₊₁y^k-1+(k+2)(k+1)aₖ₊₂y^k+...代入(14.7)

(2a₂+6a₃y+12a₄y²+...)-2y(a₁+2a₂y+3a₃y²+...)+(ε-1)(a₀+a₁y+a₂y²+...)=0 →

(2a₂+(ε-1)a₀)+[6a₃-2a₁+(ε-1)a₀]y+[12a₄-4a₂+(ε-1)a₂]y²+...=0 →

2a₂+(ε-1)a₀=0, 6a₃-2a₁+(ε-1)a₁=0, 12a₄-4a₂+(ε-1)a₂=0,..., (k+2)(k+1)aₖ₊₂-2kaₖ+(ε-1)aₖ=0

aₖ₊₂/aₖ=-[(ε-1)-2k]/[(k+2)(k+1)] 遞迴關係 , if k→∞, aₖ₊₂/aₖ=2/k

f(y)=a₀(1+a₂y²/a₀+a₄a₂y⁴/a₂a₀+...)+a₁(y+a₃y³/a₁+a₅a₃y⁵/a₃a₁+...), 也可用e^y²來表示f(y)

e^y²=1+y²+y⁴/2!+y⁶/3!+...+y^k/(k/2)!+y^k+2/(k/2+1)!+..., aₖ₊₂/aₖ=[1/(k/2)!]/[1/(k/2+1)!]=1/(k/2+1)≈2/k

改寫成f(y)=a₀Ke^y²+a₁Kye^y², 當y→∞, f(y)→∞因此令(ε-1)-2k=0,使f(y→∞)收斂

所以ε=E/(½ℏω)=2n+1, n=0,1,2,... ⸫Eₙ=(n+½)ℏω, n=0,1,2,...

ψ=(a₀Ke^y²+a₁Kye^y²)e^-y²/2, y=x/α, α²=ℏ/(mk)^½

Hermites方程式與多項式

H_υ(y)=(-1)^υe^y²(d^υ/dy^υ)e^-y² 多項式, H_υ"-2yH_υ+2υH_υ =0 方程式 υ=0,1,2,3,...

H₀=1, H₁=(-1)¹e^y²(d/dy)e^-y²=2y, H₂=(-1)²e^y²(d²/dy²)e^-y²=4y²-2, H₃=(-1)³e^y²(d³/dy³)e^-y²=8y³-12y,...

→ H_{υ +1}=2yH_υ -2υH_υ-1 遞迴關係

important integral: ∫_₋∞^∞e^y²H_υH_υdy=0, if υ≠υ or =π^½2^υυ! if υ=υ

f"-2yf+(ε-1)f=0與Hermites方程式比較, ψ=f(y)e^-y²/2波函數解中的f(y)可以H_υ(y)取代

ψ_υ=N_υH_υ(y)e^-y²/2, ∫_₋∞^∞ψ_υ²dx=1 (⸪dy=dx/α) → αN_υ²∫_₋∞^∞H_υ²(y)e^-y²dy=αN_υ²(π^½2^υυ!)=1, N_υ=1/(απ^½2^υυ!)^½

(14.6)eigenfunction ψ_υ=1/(απ^½2^υυ!)^½H_υ(x/α)e^-x²/2α², α²=ℏ/(mk)^½ eigen value E_υ=(υ+½)ℏω, υ=0,1,2,...

ex. find the normalized ψ₀

ψ₀=N₀H₀(y)e^-y²/2=N₀e^-y²/2 , ∫_₋∞^∞ψ₀²dx=1 ⸫ αN₀²∫_₋∞^∞e^-y²dy=1, N₀=(1/α√π)^½ → ψ₀=(1/α√π)^½e^-y²/2 i.e. ∫_₋∞^∞e^-z²dz=√π pf: set ∫_₋∞^∞e^-x²dx=∫_₋∞^∞e^-y²dy=I, I²=∫_₋∞^∞e^-x²dx∙∫_₋∞^∞e^-y²dy=∫_₋∞^∞∫_₋∞^∞e^-x²e^-y²dxdy 進行座標轉換, ⸪ x=rcosθ, y=rsinθ → dxdy=rdθdr ⸫∫_₋∞^∞∫_₋∞^∞e^-(x²+y²)dxdy=∫₀^2π∫₀^∞e^-r²rdrdθ=∫₀^2π(-e^-r²/2)|₀^∞dθ=½∙2π=π 因此∫_₋∞^∞e^-x²dx=√π

觀察簡諧運動的波函數,當它在基態(υ=0)時,波函數為N₀e^-y²/2, 所以機率密度如鐘形的高斯分佈N₀²e^-y²,符合古典描述:粒子在平衡位置的振動(零點運動);當量子數變大,波函數的最大振幅往位移的極限靠近,在古典中發現粒子最可能被找到的位置就是迴轉點,此時V=E也是速度最慢的時候

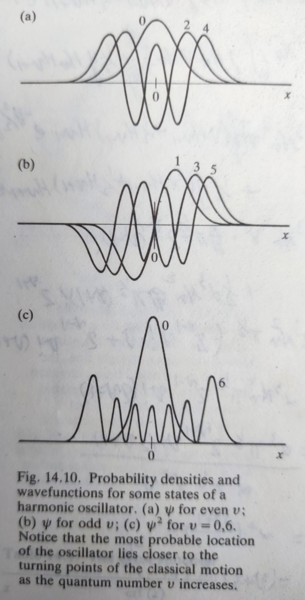
期望值: O=∫_₋∞^∞ψ^*Ȏψdx=N_υ²∫_₋∞^∞(H_υ(y)e^-y²/2)Ȏ(H_υ(y)e^-y²/2)dx

ex. mean displacement x, and mean square displacement x².

x=∫_₋∞^∞ψ_υxψ_υdx=N_υ²∫_₋∞^∞(H_υ(y)e^-y²/2)x(H_υ(y)e^-y²/2)dx=α²N_υ²∫_₋∞^∞H_υyH_υe^-y²dy

利用H_{υ +1}=2yH_υ -2υH_υ-1 遞迴關係, →α²N_υ²∫_₋∞^∞H_υ(½H_{υ +1}+υH_υ-1)e^-y²dy=½α²N_υ²∫_₋∞^∞H_υH_{υ +1}e^-y²dy+ υα²N_υ²∫_₋∞^∞H_υH_υ-1e^-y²dy=0, ⸪ ∫_₋∞^∞e^y²H_υH_υdy=0, if υ≠υ or =π^½2^υυ! if υ=υ ⸫ x=0

x²=N_υ²∫_₋∞^∞(H_υ(y)e^-y²/2)x²(H_υ(y)e^-y²/2)dx=α³N_υ²∫_₋∞^∞H_υy²H_υe^-y²dy=α³N_υ²∫_₋∞^∞H_υy(½H_{υ +1}+υH_υ-1)e^-y²dy =½α³N_υ²∫_₋∞^∞H_υyH_{υ +1}e^-y²dy+υα³N_υ²∫_₋∞^∞H_υyH_υ-1e^-y²dy=½α³N_υ²∫_₋∞^∞H_υ(½H_{υ +}₂+(υ+1)H_υ)e^-y²dy+υα³N_υ²∫_₋∞^∞H_υ(½H_υ +(υ-1)H_υ-₂)e^-y²dy=(υ+½)α³N_υ²∫_₋∞^∞H_υH_υe^-y²dy=(υ+½)α³N_υ²(π^½2^υυ!)=(υ+½)α²

平均位能V=½kx²=½(υ+½)ℏk/(mk)^½=½(υ+½)ℏω, 前面以求出E_υ=(υ+½)ℏω

因此平均動能T=E_υ-V=½(υ+½)ℏω

virial theorem: if the potential energy of a particle the form V=ax^b, then its mean potential and kinetic energies are related by 2T=bV.

依照古典力學,簡諧運動中粒子在迴轉點x_tp時,動能為零而位能等於總能,所以½kx_tp²=E;但波函數在x_tp不會突然停止,會隨位移增加逐漸歸零,因此可以計算粒子存在於|x-x_tp|>0的機率

P(x>x_tp)=2∫_xₜₚ^∞ψ²dx, x_tp=(2E/k)^½ →y_tp=x_tp/α=(2E/k)^½/[ℏ/(mk)^½]^½=(2υ+1)^½; if ground state(υ=0)

P(x>x_tp)=2∫_xₜₚ^∞ψ₀²dx=2αN₀²∫_yₜₚ^∞(H₀(y)e^-y²/2)dy=(2/√π)∫_₁^∞e^-y²/2dy

def: error function erf(z)=1-(2/√π)∫_z^∞e^-y²/2dy, P(x>x_tp)=1-erf(1)=1-0.843=0.157 當量子數υ增加,P就很快遞減歸零,符合古典的現象

3. 轉動: 分成二維和三維的轉動

假設一粒子m作圓周運動,總能等於動能E=p²/2m, 角動量l=rp(r是半徑), E=l²/2mr²=l²/2I. i.e. I=mr² 稱為動量慣性,稍後會說明角動量與能量一樣,也是量子化

因為角動量有關於粒子波函數的波長(l=rp, and p=h/λ),波長越短則角動量越大,若是波長可微任意數值,會發生波函數繞圓周運動回到原點產生不連續的情況;只有在圓周長等於波長整數倍時,波函數才能連續循環, 也就是: λ=2πr/n, n=0,1,2,... l=hr/λ=nhr/2πr=nℏ, E=n²(ℏ²/2I),此外角動量與動量一樣具有方向性,也有正負號.

二維的波動方程式(V=0): (-ℏ²/2m)[(∂²ψ/∂x²)+(∂²ψ/∂y²)]=Eψ, ²=(∂²/∂x²)+(∂²/∂y²)

座標轉換ψ(x,y)→ψ(r,ϕ), x=rcosϕ, y=rsinϕ ⸫ ²=1/r(∂/∂r)r(∂/∂r)+1/r²(∂²/∂ϕ²)

因為r=constant, (-ℏ²/2mr²)(∂²ψ/∂ϕ²)=Eψ, I=mr² or d²ψ/dϕ²=-(2IE/ℏ²)ψ

ψ=(1/2π)^½e^imₗϕ, mₗ=±(2IE/ℏ²)^½, i.e. A²∫₀^2πe^-imₗϕe^imₗϕdϕ=1, A²∙2π=1, A=(1/2π)^½

由於連續循環的緣故,ψ(ϕ+2π)=ψ(ϕ), ψₘ_ₗ(ϕ+2π)=(1/2π)^½e^{imₗ(ϕ+2π)}=(1/2π)^½e^imₗϕe^2πimₗ=ψₘ_ₗ(ϕ)e^2πimₗ

e^iπ=-1, 2mₗ=2n, n=0,±1,±2,... ⸫mₗ=0,±1,±2,... → Eₘ_ₗ=mₗ²ℏ²/2I and l=mₗℏ

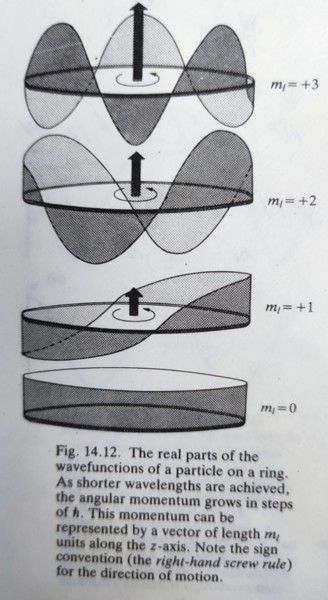
當|mₗ|增加,波長會遞減,而且波函數的結點數隨角動量增加;古典力學的角動量定義: l_z=xp_y-yp_x

p_x與p_y分別平行x軸,y軸的線動量,其算子為Ṕᵢ=-iℏ(d/di), 所以z軸角動量的算子 l_z=-iℏ[x(∂/∂y)-y(∂/∂x)],換成極座標的話,變成l_z=-iℏ(∂/∂ϕ)

ex. l_zψₘ_ₗ=-iℏ(∂(1/2π)^½e^imₗϕ/∂ϕ)=-iℏ(1/2π)^½imₗe^imₗϕ=mₗℏψₘ_ₗ,ψₘ_ₗ就是角動量l_z 的特徵函數,而mₗℏ即是相應的角動量,其正負由mₗ決定(順時針為正,逆時針為負)

機率密度: ψₘ_ₗ^*ψₘ_ₗ=(1/2π)^½e^imₗϕ(1/2π)^½e^-imₗϕ=1/2π, 為常數表示粒子位置的機率與角度ϕ 無關,即粒子位置非特定;角動量和角度是一組互補的觀察量,符合測不準原理

三維轉動: 考慮一質點自由在球面上運動,其波函數可符合通過極點和赤道的路徑,此種模型類似原子中的電子,以及轉動的分子. 波動方程式: (-ℏ²/2m)²ψ+Vψ=Eψ,²=∂²/∂x²+∂²/∂y²+∂²/∂z²

由於粒子運動的半徑r是固定的,轉換成球面極座標, ²=1/r(∂²/∂r²)r+(1/r²)Λ²,

Λ²=(1/sin²θ)(∂²/∂ϕ²)+(1/sinθ)(∂/∂θ)sinθ(∂/∂θ), 因為r和V在球面上都是常數,故方程式可簡化成:(-ℏ²/2mr²)Λ²ψ=Eψ, I=mr² → Λ²ψ=-(2IE/ℏ²)ψ (14.8), ψ=ψ(θ,ϕ)

解方程式: 令ψ(θ,ϕ)=Θ(θ)Φ(ϕ)代入(14.8), Λ²ψ={(1/sin²θ)(∂²/∂ϕ²)+(1/sinθ)(∂/∂θ)sinθ(∂/∂θ)}ΘΦ =(1/sin²θ)Θ(∂²Φ/∂ϕ²)+Φ(1/sinθ)(∂/∂θ)sinθ(∂Θ/∂θ)=-(2IE/ℏ²)ΘΦ 同除以ΘΦ,

→ (1/sin²θ)(Φ"/Φ)+(1/Θ)(1/sinθ)(∂/∂θ)sinθΘ=-2IE/ℏ² 再乘以sin²θ,

→ (Φ"/Φ)+(1/Θ)sinθ(∂/∂θ)(sinθΘ)=-(2IE/ℏ²)sin²θ, 第一項只與ϕ有關,其餘與θ 有關

可以令 Φ"/Φ=-mₗ² (14.9), →sinθ(∂/∂θ)(sinθΘ)+[(2IE/ℏ²)sin²θ-mₗ²]Θ=0 (14.10)

(14.9)循環的邊界條件Φ(ϕ+2π)=Φ(ϕ), Φ=(1/2π)^½e^imₗϕ, mₗ=0,±1,±2,... 但是(14.10)的邊界條件也會限制mₗ可以取的值

(14.10)先轉換變數, set t=cosθ, 2IE/ℏ²=l(l+1) → ∂/∂θ=(∂t/∂θ)(∂/∂t)=-sinθ(∂/∂t)=-(1-t²)^½(∂/∂t)

(14.10)→ -(1-t²)(∂/∂t)[-(1-t²)(∂Θ/∂t)]+[l(l+1)(1-t²)-mₗ²]Θ=0, ⸪Θ=(∂Θ/∂t)(∂t/∂θ)=-sinθ(∂Θ/∂t)

→ -(1-t²)[2t(∂Θ/∂t)-(1-t²)(∂²Θ/∂t²)]+[l(l+1)(1-t²)-mₗ²]Θ=0,

→ (1-t²)(∂²Θ/∂t²)-2t(∂Θ/∂t)+[l(l+1)-mₗ²/(1-t²)]Θ=0 Lgendre equation

方程式解Θ_l,|mₗ|須滿足兩個條件: (a)l=0,1,2,... (b)|mₗ|<l 才是可接受的且不發散的解

粒子在球面上的波函數,Y_l,mₗ=NΘ_l,|mₗ| Φ_mₗ with l=0,1,2,... and mₗ=0,±1,±2,...±l

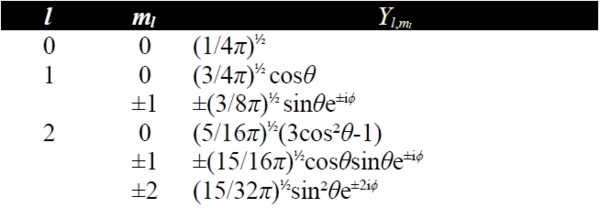
(1)粒子的能量: E=l(l+1)ℏ²/2I, l=0,1,2,... 能量量子化,l是量子數而mₗ與能量無關

(2)已知l,根據條件(b)|mₗ|<l, mₗ=0,±1,±2,...±l 或者2l+1個mₗ值,也就是有2l+1個不同mₗ值的波函數,但這些波函數都相應同一個能量; 表示l能階有2l+1個簡併能態

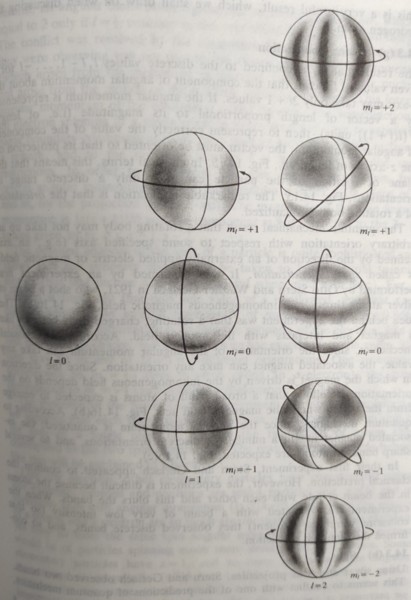
(3)角動量: 其值等於[l(l+1)]^½ ℏ, l=0,1,2,... 一樣是量子化;z軸角動量=mₗℏ, mₗ=0,±1,±2,...±l

(4)波函數ψ_l,mₗ=Y_l,mₗ(θ,ϕ)稱為球諧函數(spherical harmonics), Y_l,mₗ=NΘ_l,|mₗ| Φ_mₗ 當l增加,結線數也跟著增加,也意味角動量與能量隨l增大,波函數變得更彎曲

(5)滿足球諧函數的微分方程式: Λ²Y_l,mₗ=-l(l+1)Y_l,mₗ

空間量子化: 由波函數與其量子數,顯示mₗ限定在l,l-1,..,0,-1,...,-l的離散數值,L_z只允許2l+1個值,角動量大小與向量長度成比例,向量投影在z軸的長度可以代表|mₗ|,表示旋轉粒子的指向也是量子化;量子力學顯示旋轉物體相對於特定軸,不能有任意的指向,此現象稱為空間量子化

Stern-Gerlach實驗: 根據古典力學,角動量的指向可取任意值,受磁場影響的磁矩會呈現寬帶連續的粒子分布;而量子力學因角動量量子化的緣故,會有分離的帶狀粒子分布

SGE利用狹縫分離出銀原子束,通過不均勻的上下磁場,得到二條分離的帶狀圖形;不過這與l角動量有2l+1個指向的說法衝突,因此實驗結果並不是因為原子軌道角動量造成的,而是來自

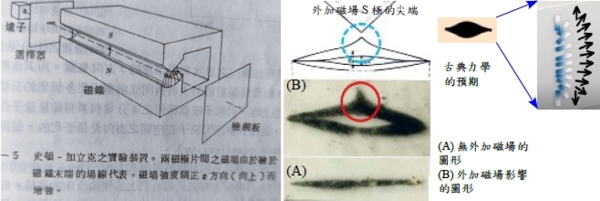
於電子的自旋角動量S,為了區別軌道角動量的量子數l與mₗ,以s與mₛ替代,自旋角動量S=[s(s+1)]^½ ℏ, z軸自旋角動量S_z=mₛℏ, mₛ=s,s-1,s-2,...,-s

對一個電子只有允許一個s值,s=½相應的自旋角動量S=(√3/2)ℏ=0.866ℏ,自旋可以有2s+1=2個指向: mₛ=+½(α電子),和mₛ=-½ (β電子),即可對應SGE實驗結果

ex. spin-½ particles(i.e. s=½)are protons and neutrons,their S=(√3/2)ℏ but mch slow than electron due to mass. Spin-1 particles are mesons and photons, S=√2ℏ.

Vector model for 角動量:

軌道角動量量子數: l (l=0,1,2,...), z軸量子數(也稱磁量子數): mₗ (mₗ=0,±1,±2,...±l)

自旋角動量量子數: s (s=½ for an electron), z軸量子數: mₛ (mₛ=±½ for an electron)

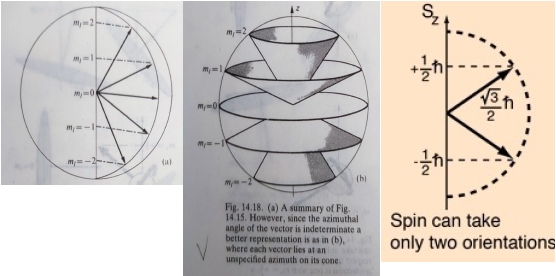
Q: 關於角動量的方向,為何只關注z方向的角動量l_z ,那l_x 和l_y呢? 由於測不準原則,不允許超過一個以上的變量同時被精確的認定

ex. confirm that the following wavefunctions ψ_l,mₗ for a particle on a spherical surface satisfy the Schrodinger eq., and that in each case the energy and angular momentum of the particle are given by E=l(l+1)ℏ²/2I and L=[l(l+1)]^½ ℏ. (a)ψ₀_,₀=1/2π^½ (b)ψ₂_,₋₁=(15/16π)^½cosθsinθe⁻^iϕ (c)ψ₃_,₃=-⅛(35/π)^½sin³θe³^iϕ

滿足球諧函數的微分方程式: Λ²Y_l,mₗ=-(2IE/ℏ²)Y_l,mₗ , Λ²=(1/sin²θ)(∂²/∂ϕ²)+(1/sinθ)(∂/∂θ)sinθ(∂/∂θ)

(a)ψ₀_,₀=1/2π^½ 為常數, 所以Λ²ψ₀_,₀=0=-(2IE/ℏ²)ψ₀_,₀, 表示E=0, and L=0(⸪L=[l(l+1)]^½ ℏ, and E=l(l+1)ℏ²/2I)

(b)Λ²ψ₂_,₋₁=(1/sin²θ)(∂²ψ₂_,₋₁/∂ϕ²)+(1/sinθ)(∂/∂θ)sinθ(∂ψ₂_,₋₁/∂θ)

∂ψ₂_,₋₁/∂θ=(15/16π)^½e⁻^iϕ∂cosθsinθ/∂θ=(15/16π)^½e⁻^iϕ(cos²θ-sin²θ)

(1/sinθ)(∂/∂θ)sinθ(∂ψ₂_,₋₁/∂θ)=(1/sinθ)(∂/∂θ)sinθ(15/16π)^½e⁻^iϕ(cos²θ-sin²θ)=(15/16π)^½e⁻^iϕ/sinθ(∂/∂θ) sinθ(cos²θ-sin²θ)=(15/16π)^½e⁻^iϕ/sinθ[cos³θ-5cosθsin²θ]=(15/16π)^½e⁻^iϕ[cosθ/sinθ-6cosθsinθ], ⸪cos³θ=cosθ(1-sin²θ)

(1/sin²θ)(∂²ψ₂_,₋₁/∂ϕ²)=(15/16π)^½cosθsinθ/sin²θ(∂²e⁻^iϕ/∂ϕ²)=-(15/16π)^½cosθe⁻^iϕ/sin²θ

→ Λ²ψ₂_,₋₁=-(15/16π)^½e⁻^iϕ 6cosθsinθ=-6ψ₂_,₋₁=-2(2+1)ψ₂_,₋₁, l=2

-6ψ₂_,₋₁=-(2IE/ℏ²)ψ₂_,₋₁, E=3ℏ²/I; L=[l(l+1)]^½ ℏ=√6ℏ

(c)Λ²ψ₃_,₃=(1/sin²θ)(∂²ψ₃_,₃ /∂ϕ²)+(1/sinθ)(∂/∂θ)sinθ(∂ψ₃_,₃/∂θ)

∂ψ₃_,₃/∂θ=-⅛(35/π)^½(3sin²θcosθ)e³^iϕ

(1/sinθ)(∂/∂θ)sinθ(∂ψ₃_,₃/∂θ)=-⅛(35/π)^½e³^iϕ/sinθ(∂/∂θ)sinθ(3sin²θcosθ)=-⅛(35/π)^½e³^iϕ[9sinθcos²θ-3sin³θ]=-⅛(35/π)^½e³^iϕ3sinθ(3cos²θ-sin²θ)=-⅛(35/π)^½e³^iϕ3sinθ(3-4sin²θ)

(1/sin²θ)(∂²ψ₃_,₃/∂ϕ²)=-⅛(35/π)^½sinθ(∂²e³^iϕ/∂ϕ²)=⅛(35/π)^½sinθ(9e³^iϕ)

Λ²ψ₃_,₃=⅛(35/π)^½e³^iϕ(12sin³θ)=-12ψ₃_,₃=-3(3+1)ψ₃_,₃, l=3

-12ψ₃_,₃=-(2IE/ℏ²)ψ₃_,₃, E=6ℏ²/I; L=[l(l+1)]^½ ℏ=√12ℏ